【明報專訊】小時候,如果有同學跟你同一天生日,你會驚訝這麼巧!感覺跟他特別有緣,倍感親切。這只是一種巧合?當你知道一班50人,有兩同學同一天生日的機會率其實高達97%!你就不會覺得浪漫了。日常生活中,面試、談戀愛、等巴士、買六合彩、股票預測、天氣預告、解讀新聞數字資訊等,都涉及到機率學,眼見未為真,直覺亦不可靠,稍一不慎,隨時做錯決定或被誤導。
三道門,揀中房車的機會是……
試想像自己置身於電視台的遊戲節目,在三道門中,你可選擇打開其中一道門,當中一道門是名貴房車,其餘兩道門是山羊。當你選定了一道門(假設是A門),揭曉前,主持人打開另一道(假設是C門),裏頭是山羊,然後問你,你會否考慮選擇另一道門?改變選擇會否對自己有利?很多人認為,即使改變主意,贏得汽車的機會也是1/2。這是著名的蒙提霍爾問題(Monty Hall problem),曾引起熱烈討論,原來改變主意的話,贏的機會是2/3。
「人的直覺常出現誤判。」香港大學統計及精算學系副教授楊良河說。日常許多事情,我們常被直覺或接觸到的資訊所影響,未能作出理想的決定。
必勝法存在嗎?
世上有沒有人可以擲銀仔,輕易擲出10次「字」?連續貼中10場賽事?看似不太可能的事,有人可以做到。楊教授表示,「一個人的成功『事迹』,可以是靠實力、運氣,亦有可能是耍了一些花招。我們收到的資訊,是對方經過多次試驗中的成功例子,失敗例子沒公布而已。」
花4.5小時 成功擲到10次「公」
英國心理學研究者和魔術師Derren Brown曾在一節目中分享他的「百分百」贏馬之道。他隱藏身分,用電郵告訴一名女士Khadisha,哪一匹馬將贏取次日的賽事,一連5場賽事都預測成功。直到第6場她押上巨注時,Derren Brown跟她解釋,根本沒有必勝法存在。為什麼他有能力製造一些看似不可能的情况出現?他再次在觀眾面前做實驗,片段中,他擲硬幣,竟然能夠連續10次擲到「公」。答案其實很簡單,楊教授說,「因為他擲了許多次,以機會率計算,平均擲2046次可得到10次『公』,以每次投擲使用8秒來計,他平均要花4.5小時,但只剪輯了最後成功擲到10次公的片段出來。」
至於賭馬,他開始時聯絡了7776人,將他們分成6組,每場有6隻馬作賽,每組給一隻馬作為貼士。每場賽事會有5/6的人輸,以同樣方法,如是者經過5場比賽後,就會有一人連贏5場,這人正好是Khadisha。「如果你是Khadisha,有人可以貼中5場賽事,也會對這人的能力深信不疑。這實驗告訴我們,有時候我們受一些眼看到的『現實』所欺騙,你以為百分百準確,一定是這樣,事實卻並不一定。」楊教授說。
預測股市升跌
假如股市正醞釀熊市,金融專家跟你說,過去股災這隻股票最多只是跌20%,不用太擔心。過去表現不代表將來,過去最多跌20%是否代表將來不會跌超過20%?沒有人能夠保證。但我們常被這類資訊影響。
「不敗基金」真的存在?
楊教授表示,「好多時候我們根據過往經驗,了解當中的可行性、發生的機會率,但這並非是一個好的預測。例如買一隻基金前,會了解它過去的表現,但這些都是過去的資訊,過去10年都升,不能保證第11年也會升。曾經有一基金,每一年也穩定獲利,連續13年無敗績,被譽為「不敗基金」,但這不敗神話在數年前破滅。做任何分析或預測時,不可單憑過去表現作決定。要作出正確判斷,需要了解對方是否用合適的數據,要認識統計方法及其背後的假設是否恰當,避免用直覺或過去形態作判決。」
認識機會率 改變看法
即使失敗也不要放棄,終有一天會成功!這種勉勵說話,從小聽到大,你未必上心,然而從機會率的角度,能夠證明這說法是對的。《你的人生,需要多懂一點機率》一書作者野口哲典舉例,假設你對某件事情的把握只有50%,成功和失敗的比率各佔50%。
而我們嘗試5次都失敗的機會率為每次失敗機會率50%的5次方,即0.55 = 0.03 = 3%,故5次嘗試中,有一次會成功的機會率為100%-3%,即是高達97 %!結論是,嘗試5次便很大機會成功。
但這程式,並不適用於任何情况。
例如醫生跟你說,做這個手術有一半機會成功,如果連續做數次,成功率便大增?楊教授解釋,「成功率一半,只是說第一次手術的成功率而已,而並非每次手術的成功率。打個比喻,在一大班人中,患心臟病的機會率相對很小,但對於某一類人的話,例如高血壓、肥胖的人等,患心臟病的風險大增,手術成功率多少,背後要很多因素要考慮。不過,人很多時以簡單的方法思考,墮入機率陷阱」。
買六合彩 電腦飛易中啲?
有人覺得一直買同一組號碼,總有天會中獎,有些人則買不同號碼或電腦飛,事實上,不管是用哪一種方法,中獎機會率是一樣。那麼,有沒有比較易中獎的數字?有人會留意過去十期的中獎號碼,推測什麼號碼較易中。參考之前的中獎號碼根本沒意義,因為中獎機會率都是一樣,以六合彩而言,第一個數字是1/49,第二個數字是1/48,如此類推。
絕對風險vs.相對風險
英國藥物安全協會在一九九九年的新聞發布會,公布的資訊曾引起恐慌。他們稱第三代口服避孕藥造成血栓塞致死的風險,是過去的兩倍,亦即是血栓塞的風險提高了百分之百,很多婦女因而自行停藥而不小心懷孕。德國心理學家Gerd Gigerenzer在《機率陷阱》一書提到,「許多專家,包括醫生、律師、財務顧問與政府官員,常常比我們想像中更容易誤解統計數字,讓我們被錯誤的資訊與無畏的恐懼所誤導」。
風險提高百分之百,到底有多大?
上述例子,Gerd Gigerenzer反問,風險提高了百分之百,到底是多大風險?研究指出,每7000名服用口服避孕藥的婦女,約有一個會出現血栓塞;而在7000名服用第三代避孕藥的婦女中,約有兩個出現血栓塞。換言之,第三代口服避孕藥造成血栓塞的「絕對風險」只是增加了七千分之一;但相對風險比前一代避孕藥增加了百分之百。新聞報道亦經常製造這類恐慌,作者認為,要消除疑慮,判讀風險時要思考「絕對風險」增加率到底有多少?
認清分母 基數不同
報道:「據考評局資料,2017年中學文憑試(DSE)中,3.4%考生在中文科考獲5*或以上,英文科有3.8%。同時在中英文考獲5*或以上的考生則有3.6%。」只有3.4%考生中文摘星,為何中英文同時摘星的考生會超過3.4%?
楊教授解釋,「可能性之一,是兩者計算的分母不一樣。3.4%是計算只有報考中文科的人,而3.6%是計算所有報考中文及英文科的人,計算的分母不同,故會出現這誤會。」
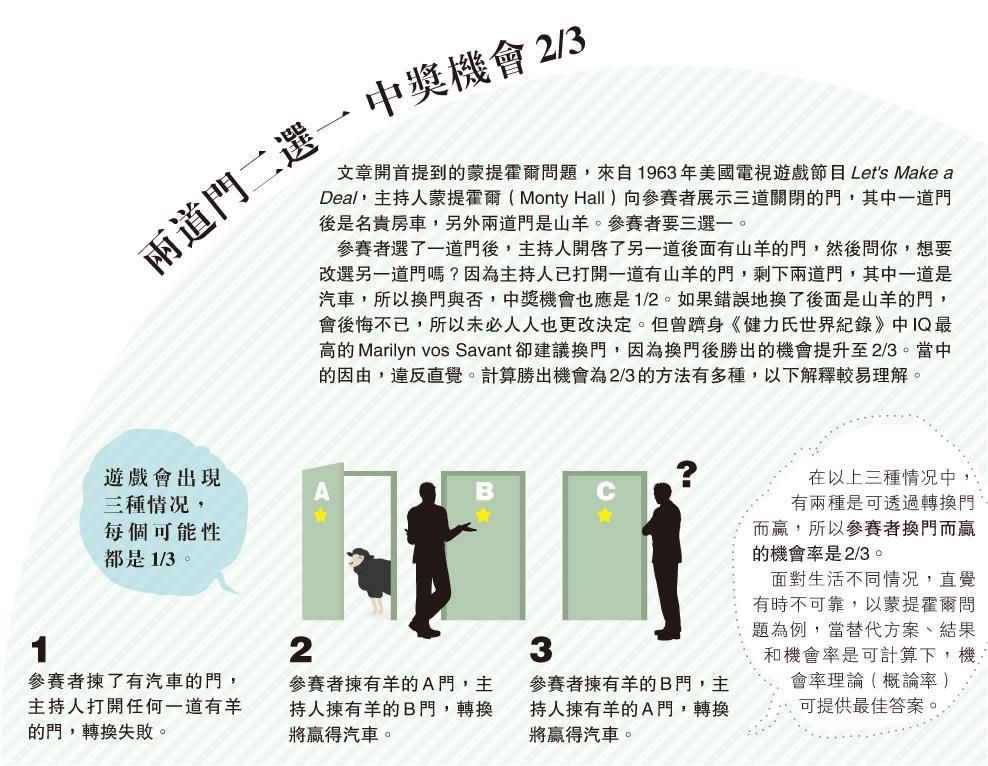
兩道門二選一 中獎機會2/3
文章開首提到的蒙提霍爾問題,來自1963年美國電視遊戲節目Let's Make a Deal,主持人蒙提霍爾(Monty Hall)向參賽者展示三道關閉的門,其中一道門後是名貴房車,另外兩道門是山羊。參賽者要三選一。
參賽者選了一道門後,主持人開啟了另一道後面有山羊的門,然後問你,想要改選另一道門嗎?因為主持人已打開一道有山羊的門,剩下兩道門,其中一道是汽車,所以換門與否,中獎機會也應是1/2。如果錯誤地換了後面是山羊的門,會後悔不已,所以未必人人也更改決定。但曾躋身《健力氏世界紀錄》中IQ最高的Marilyn vos Savant卻建議換門,因為換門後勝出的機會提升至2/3。當中的因由,違反直覺。計算勝出機會為2/3的方法有多種,以下解釋較易理解。(見圖二)